El nacimiento de los números como entes abstractos se pierde en la noche de los tiempos. Quisiera presentar los números que considero, según mi modesta opinión, los representantes de la historia de las ciencias exactas, así que empezaré por los primeros números Naturales o conjunto N. Hace unos cinco mil años parece ser que más de dos ya eran muchos, así que en Mesopotamia al número tres se le denominaba “es”, que también se utilizaba para indicar los plurales, como nosotros utilizamos el sufijo “es” en el idioma castellano. El primer número que se manifestó ante nosotros fue el 1, junto con el 2 cuando fuimos capaces de identificarnos como entidades separadas del resto: Yo y el Mundo. Antes de que los números existieran para contar se realizaban incisiones en huesos, en objetos de arcilla, etc, los vestigios más antiguos de esta forma de contar datan del 35.000 a.c. en las montañas Lembedo de África.

Con la aparición de los Pitagóricos los números adquirieron vital importancia hasta el punto de ser la materia primordial de su filosofía. En esa época, a partir del siglo VI a.c., los números Naturales ya se contaban en base 10 derivando probablemente de que tengamos diez dedos, y los números pares estaban asociados con la feminidad, así como los impares lo estaban con los atributos masculinos.

Después de los números naturales tenemos a los Racionales o conjunto Q, o lo que es lo mismo aquellos números que pueden ser representados como la proporción o fracciones de dos números Naturales. Los números racionales cumplen con la función arquimediana o de densidad, es decir para cualquier pareja de números racionales podemos encontrar otro número racional. Mi representante de los números racionales lo obtendré de los dos primeros números Naturales escogidos, es decir el ½ o 0,5. Los griegos y egipcios tenían dificultades con los números racionales con numerador distinto de uno, a diferencia de los romanos que utilizaron fracciones con cualquier numerador. El papiro egipcio Rhind, que es anterior al 1650 a.c., muestra nombres de fracciones donde el numerador es 1.

Los Pitagóricos descubrieron a los siguientes protagonistas, los números irracionales o inconmensurables, estos son números con infinitas cifras decimales no periódicas que no pueden ser representados como fracciones de dos números Naturales. Los Pitagóricos intentaron mantener en secreto su descubrimiento porque iba en contra de su creencia de que los números eran entes perfectos que gobernaban el Universo. Mis representantes de los números irracionales serán la raíz de dos como resultado más simple del teorema de Pitágoras donde la hipotenusa de un triangulo cuyos catetos miden la unidad da como resultado ese mismo número, otro representante será ? que es el valor del cociente entre la longitud de la circunferencia y la longitud de su diámetro. Las primeras aproximaciones al número pi fueron realizadas por los egipcios utilizando fracciones de números Naturales alrededor del 1650. a.c, y con Arquímedes en el siglo III a.c. empiezan las mejores aproximaciones de pocos decimales. En nuestra época gracias a los ordenadores se alcanzan billones de decimales. Otro representante de los irracionales, no menos importante y decisivo, fue el número áureo o número ? (pronunciado como fi), siendo el resultado de la división de un segmento en media extrema y razón, también denominada proporción áurea. La unión de los racionales e irracionales nos llevan a los números Reales o conjunto R.

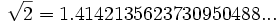
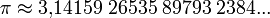
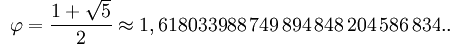
Los siguientes protagonistas de la historia de los números son los números negativos y el cero, dando paso a los números enteros o conjunto Z al unirse a los números Naturales. Llegado a este punto elijo como representantes al 0 y al -1. El cero como un número en si mismo no empezó a utilizarse hasta el siglo VII d.c. en la India. Antes, por ejemplo en Mesopotamia, sólo se utilizaba como indicador de lugar vacío en nuestro sistema numérico de valor por posición, por ejemplo el cero que aparece en el número 108, pero no como número independiente. Los matemáticos indios, entre ellos Brahmagupta, dieron las reglas de la aritmética para el cero y los números negativos. Estas nuevas ideas viajaron a otros lugares, como a China o a los países islámicos, hasta que estos sistemas numéricos llegaron a Europa. El matemático italiano Fibonacci (s. XII – XIII) fue uno de los principales responsables. Pero una de las más conocidas contribuciones a las matemáticas que hizo este matemático italiano fue la serie de Fibonacci que estaba relacionada con el número ?.

Los siguientes en aparecer son los números complejos o conjunto C. Estos números son el resultado de raíces cuadradas de números negativos y empezaron a ser ampliamente conocidos a partir del siglo XVI gracias a matemáticos como Tartaglia o Cardano. Los números complejos constan de una parte real y una parte imaginaria, donde la unidad imaginaria es denominada número i o raíz cuadrada de -1. El matemático Euler (s. XVIII), en su formula que lleva su nombre, utilizó la unidad imaginaria y otro número no menos importante, el número e o base del logaritmo natural. Estos números se usan en la actualidad en multitud de campos, por ejemplo en la ingeniería electrónica o en la mecánica cuántica. Los números Reales están incluidos en los complejos.

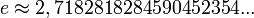
Repetimos: 1, 2, ½, raíz de dos, ?, ?, 0, -1, i, e

Y ahora para acabar, una demostración matemática. Si 1/3 es igual a 0,3333… y 0,3333… + 0,3333… + 0,3333… = 0,9999… Y por otro lado tenemos que 3*1/3 = 1. ¿1 es igual a 0,9 periódico?.